Zahlenzauber - Der PCR-Test und die Zahlen

Die Zahlen des RKI zu den positiv Getesteten wird seit Monaten als Grundlage für sämtliche Argumentationen über die Gefährlichkeit des SARS-CoV-2 Virus herangezogen. Weiterhin bildet diese Zahlenbasis die Entscheidungsgrundlage für alle einschränkenden Maßnahmen bis hin zum Lockdown. Jedoch ist die Aussagekraft der veröffentlichten Zahlen alles andere als hoch und wissenschaftlich nicht nachvollziehbar, da wesentliche Kennzahlen nicht veröffentlicht werden, oder nicht bekannt sind. Dies macht eine sichere Bestätigung oder Widerlegung der RKI-Interpretation unmöglich. Ist das evtl. gewollt, oder gibt es diese Kennzahlen innerhalb des RKI überhaupt nicht, was im Endeffekt noch fataler wäre. Denn ohne diese Kennzahlen sind die präsentierten Zahlen schlicht Restmüll, der in die Tonne gehört. Nachfolgend soll die Zahl der positiv Getesteten im Rahmen der Möglichkeiten auf ihre Aussagekraft hin überprüft werden....
Die für die PCR-Tests eigentlich hoch relevanten Kennzahlen Sensitivität und Spezifität werden allerdings wie ein Goldschatz vom RKI unter Verschluss gehalten. Daher müssen bei der hier dargelegten Überprüfung Annahmen herangezogen werden, die kritische Wissenschaftler bezüglich dieser Zahlen getroffen haben. Der Einfachheit halber wird für die weiteren Ausführungen der Sprachgebrauch übernommen, der positive Getestete als „Infizierte“ bezeichnet. Der berechtigten Fragestellung, ob der Test überhaupt Infizierte bzw. eine eindeutige Infektion mit SARS-CoV-2 nachweisen kann, soll hier nicht nachgegangen werden. Dazu an anderer Stelle mehr.
Erklärung der Begrifflichkeiten:
| Sensitivität: | wieviel Prozent der wirklich Infizierten erkennt der Test als „infiziert“ bzw. sind „positiv“. Das ist die Menge der „richtig positiven“. Der Rest zu 100% sind die „falsch negativen“, d.h. deren Ergebnis ist „negativ“, obwohl sie eigentlich "positiv" sein müssten, weil infiziert. Der Wertebereich der Sensitivität geht von 0 bis 1 (1 entspricht 100%). Der realistische Bereich der Sensitivität für den PCR-Test wird von Wissenschaftlern irgendwo zwischen 0,5 und 0,9 angenommen (50% bis 90%). |
| Spezifität: | wieviel Prozent der wirklich Gesunden erkennt der Test als „gesund“ bzw. sind „negativ“. Das ist die Menge der „richtig negativen“. Der Rest zu 100% sind die „falsch positiven“, d.h. deren Ergebnis ist „positiv“, obwohl sie gesund sind, bzw. nicht infiziert. Der Wertebereich der Spezifität geht von 0 bis 1 (1 entspricht 100%). Der realistische Bereich der Spezifität für den PCR-Test wird von Wissenschaftlern irgendwo zwischen 0,99 und 0,998 angenommen (99,0% bis 99,8%). |
| Infizierte: | wieviel der positiv getesteten sind wirklich infiziert |
| Gesunde: | wieviel der negativ getesteten sind wirklich gesund |
Nachfolgend die verwendeten Begriffe und Formeln mit den Formelzeichen:
Folgende Zahlenbasis ist bekannt:
| Testzahl pro Woche: | T (Quelle: RKI - Epidemiologisches Bulletin 36/2020) |
| Anzahl positiv getestete: | P (Quelle: RKI - Epidemiologisches Bulletin 36/2020) |
Annahmen:
| Sensitivität: | Sens |
| Spezifität: | Spez |
Weitere Größen:
| richtig positive: | Rp |
| falsch positive: | Fp |
| richtig negative: | Rn |
| falsch negative: | Fn |
| Infizierte: | I |
| Gesunde: | G |
Formeln:
| Anzahl negativ getestet: | N = T - P | (1) |
| Testzahl pro Woche: | T = P + N | (2) |
| Testergebnis positiv: | P = Rp + Fp | (3) |
| Testergebnis negativ: | N = Rn + Fn | (4) |
| richtig positive: | Rp = I * Sens | (5) |
| falsch negative: | Fn = I * (1-Sens) | (6) |
| richtig negative: | Rn = G * Spez | (7) |
| falsch positive: | Fp = G * (1 - Spez) | (8) |
Formeln einsetzen und umbauen:
| wie oben definiert: | |
| P = Rp + Fp | (3) |
| Rp (5) und Fp (8) in (3) einsetzen: | |
| P = I * Sens + G * (1 - Spez) | (9) |
| aus obiger Definition: | |
| N = Rn + Fn | (4) |
| Rn (7) unf Fn (6) in (4) einsetzen: | |
| N = G * Spez + I * (1 - Sens) | (10) |
| (10) nach G umstellen: | |
| G = (N - I * (1 - Sens)) / Spez | (11) |
| (11) einsetzen in (9): | |
| P = I * Sens + ((N - I * (1 - Sens)) * (1 - Spez)) / Spez | |
| nach I umstellen ergibt: | |
| I = (P * Spez + N * Spez - N) / (Sens + Spez - 1) | (12) |
| N in (12) durch (T-P) (1) ersetzen: | |
| I = (P * Spez + T * Spez -P *Spez - T + P) / (Sens + Spez - 1) | (13) |
| Nach Vereinfachung ergibt sich: | |
| I = (T * (Spez - 1) + P) / (Sens + Spez + 1) | (14) |
| Die Anzahl der wirklich Gesunden ist dann simpel: | |
| G = T - I | (15) |
| Oder komplizierter: | |
| G = (T * Sens - P) / (Sens + Spez - 1) | (16) |
Damit haben wir nun mit (14) und (15) bzw. (16) einfache Formeln, wie wir aus der Testmenge T, der Anzahl positiv Getesteter P und den Kenngrößen Sensitivität Sens und Spezifität Spez die Anzahl der wirklich infizierten I und die Anzahl der wirklich gesunden G errechnen können. Das Wort 'wirklich' darf an dieser Stelle nicht als Abbild der Wirklichkeit verstanden werden, sondern bildet auf Basis der Wahrscheinlichkeiten für Sensitivität und Spezifität rechnerisch die Größen der entsprechenden Personengruppen ab.
Machen wir daraus ein Beispiel mit den Zahlen aus dem RKI Dokument „RKI - Epidemiologisches Bulletin 36/2020“. Auf Seite 15 lauten die Zahlen für die Kalenderwoche 32 (KW32, 03.08.2020 bis 09.08.2020) für die Anzahl Testungen T, sowie der Anzahl der positiv Getesteten P wie folgt:
| Anzahl Testungen: | T = 733.990 | (17) |
| Anzahl positiv Getestete | P = 7.330 | (18) |
Für die vom RKI nicht veröffentlichten Größen nehmen wir folgende Annahmen:
| Sensitivität: | Sens = 0,7 | (19) |
| Spezifität: | Spez = 0,993 | (20) |
Setzen wir nun die Zahlen (17) bis (20) in (13) ein, so erhalten wir für die Anzahl der:
| wirklich Infizierten: | I = 3.163,16 | gerundet: 3.163 Personen |
| wirklich Gesunden: | G = 730.826,84 | gerundet: 730.827 Personen |
Die weiteren Größen (jeweils gerundet auf volle Personen) sind:
| richtig positive: | Rp = 2.214 |
| falsch negative: | Fn = 949 |
| richtig negative: | Rn = 725.711 |
| falsch positive: | Fp = 5.116 |
Erklärung der Zahlen:
von den im RKI Bericht gemeldeten 7.330 positiv getesteten Personen ist nur bei 2.214 Personen der Test wirklich positiv. Der Rest von 5.116 Personen hat ein „falsch positives“ Ergebnis erhalten.
949 Personen sind fälschlicherweise als negativ getestet, obwohl sie eigentlich positiv sein müssten.
Rechnet man nun noch den positiven Vorhersagewert aus, der sich wie folgt ergibt:
| Vp = Rp / P * 100 [%] | (21) |
so erhält man für dieses Beispiel:
| Vp = 30,21% |
Dies bedeutet, dass der Test in KW32 nur zu 30,21 Prozent sicher sagen kann, dass eine als positiv getestete Person wirklich positiv ist!
Das ist sehr weit weg von einer 100%-igen Sicherheit, die für den Test lautstark proklamiert wird.
Ist der Test 100%ig - oder ist das eher kontraproduktiv?
Diese Zahlenwerte sind natürlich abhängig von den Annahmen zur Sensitivität und zur Spezifität. Da das RKI hierzu jedoch keine belegbaren und verifizierbaren Zahlen veröffentlicht, müssen zwangsweise Annahmen getroffen werden. Wenn man die Annahmen zur Sensitivität und Spezifität verändert, so muss man bedenken, dass dann konsequenterweise im Realen auch die Ergebnisse (Anzahl der Positiven) anders ausfallen würden. Das ist sozusagen ein Henne-Ei-Problem des nachträglichen Versuchs der Analyse. Eine klare Darlegung der Fakten durch das RKI würde die Thematik auf belastbare Beine stellen. Aber genau das wird seit Monaten vom RKI abgelehnt. Und das RKI verlangt dennoch Vertrauen in deren Arbeit und Ergebnisse?
Bei der Variation der Annahmen fällt auf, dass die Sensitivität nur einen minimalen Einfluss auf das Ergebnis der Falsch- Positiven hat. Viel relevanter ist die Spezifität. Wenn diese nahe 100% kommt, so würde das bedeuten, dass der Test nahezu alle Gesunden als gesund erkennt und nur wenige davon fälschlicherweise als Infizierte (Falsch-Positive). Damit wäre die Anzahl der positiv Getesteten in der RKI Tabelle nahezu richtig. Damit wird auch klar, warum das RKI in manchen Aussagen eine Spezifität von 100% angibt (wie im verlinkten Bulletin 36/2020). Die Zahlenbasis zu den Testungen soll demgemäß als 100% richtig definiert werden. Das widerspricht jedoch der Unterstellung vieler Kritiker, dass der Test viele positive Testfälle herbeizaubert. Die Spezifität müsste niedriger angesetzt werden, um viele Falsch-Positive zu erzeugen, die dann in der Statistik die Zahlen nach oben treiben. Das RKI ist hier wohl in einer Zwickmühle: entweder der Test ist 100% richtig damit Vertrauen in den PCR-Test gesetzt wird und die positiv-Zahlen bleiben durch die ausbleibenden Falsch-Positiven (und real nicht vorhandenen Infizierten) klein, oder der Test ist weniger spezifisch (sprich: ungenau) und die positiv-Zahlen sind aufgrund der hohen Anzahl falsch-positiver Fälle hoch, was für die Begründung der Maßnahmen und Aufrechterhaltung der Panik günstig wäre. Was tun liebes RKI? Fakten darlegen? Geht leider nicht, denn dann wäre der Zahlenzauber entblößt.
Ein Standardtest - der keinen Standard kennt
Ein weiterer entscheidender Unsicherheitsfaktor mit den Annahmen zur Sensitivität und Spezifität ist, dass es inzwischen eine sehr hohe Zahl an PCR-Tests von unzähligen Herstellern gibt. Das Bundesinstitut für Arzneimittel und Medizinprodukte listet 499 registrierte PCR-Tests (Stand 17.08.2020) mit in Spitze 183 beteiligten Diagnostiklabore, die die Tests durchführen und die Ergebnisse melden. Weiterhin sind die in den PCR-Tests verwendeten Primer nicht global definiert, so dass jeder Hersteller sein eigenes Süppchen kochen kann. Diese Primer (fast immer zwei, selten drei) geben diejenigen DNA-Abschnitte des SARS-CoV-2 Genoms vor, die der Test SARS-CoV-2-spezifisch detektieren soll. Die nächste Variable ist der ebenfalls nicht einheitlich definierte sog. Cut-Off Wert. Dieser definiert die Entscheidungsschwelle zwischen dem Ergebnis „positiv“ und „negativ“. Allgemeingültige Werte für die Sensitivität und Spezifität kann es aufgrund dieses Variantenreichtums niemals geben. Rein wissenschaftlich müssten zu jedem gemeldeten Testergebnis a) der verwendete PCR-Test, b) die Werte für Sensitivität und die Spezifität, c) der CutOff- (CT-) Wert und d) die verwendeten Primer (Genom-Marker) mit angegeben werden, um damit eine Bewertung der einzelnen Testergebnisse vornehmen zu können. Dies findet jedoch nicht statt, weil es in der Praxis überhaupt nicht umsetzbar ist. Konsequenterweise muss die gesamte Kette der PCR-Testerei als höchst unwissenschaftlich und untauglich als Grundlage für die Pandemieargumentation angesehen werden.
Die Pandemie im Bild
Das Schaubild unten zeigt, dass die Anzahl der Falsch-Positiven in der Hochzeit der Pandemie mit den o.g. Annahmen unter 10% bleibt. Jedoch weist die Anzahl der als positiv Getesteten seit KW 20 (Mitte Mai) einen Anteil von 50% bis 100% Falsch-Positiven auf. Generell gilt, dass je kleiner das Verhältnis von positiv Getesteten zur Testanzahl ist, desto höher wird der Falschanteil. Bezogen auf die Gesamtbevölkerung in D (ca. 83,2 Mio.) haben die „wirklich Infizierten“ in KW32 lediglich ein Anteil von ca. 0,004%. Selbst aufsummiert von KW10 bis KW32 spiegelt die berechnete Zahl von 276.341 Personen lediglich einen Anteil von 0,33% an der Gesamtbevölkerung wider. Diese Größenordnungen kann man nur mit viel Promille im Gehirn als (anhaltende) Pandemie bezeichnen. Ginge man noch einen Schritt weiter und würde die Anzahl wirklich Erkrankter in die Betrachtung mit einbeziehen - also diejenigen Personen mit Symptomen - dann würden die Zahlen im Sinne einer Pandemie noch unbedeutender werden.
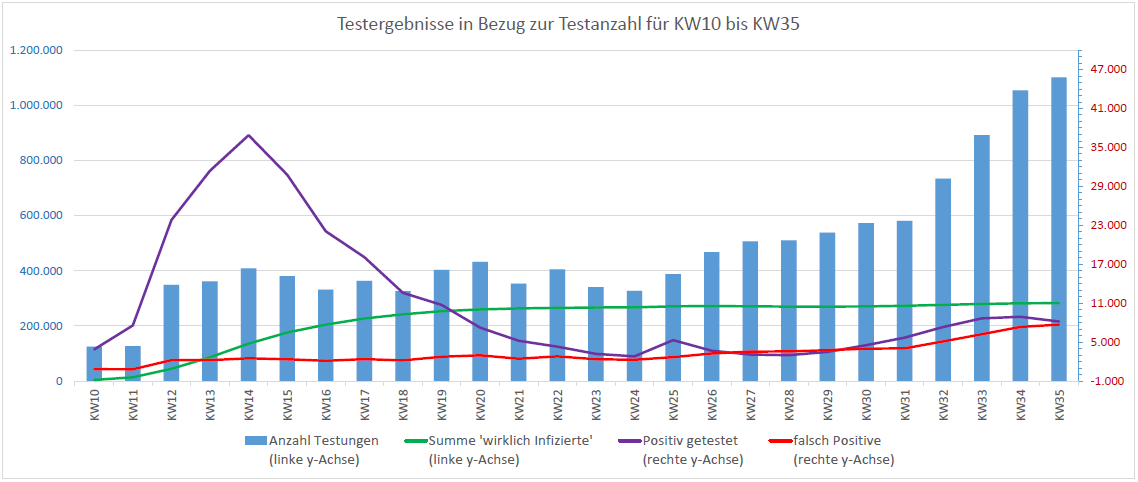
Screenshot des verwendeten Excel-Tools, das auf Basis der o.g. Formeln die Zahlen berechnet:






 telegram
telegram RSS feed
RSS feed